[통계학 기초] 선형회귀모형 Linear regression model
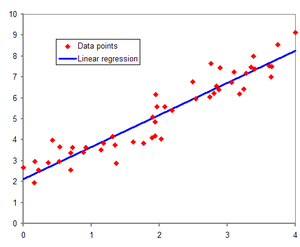
선형회귀모델 : 자료 x,y를 설명하는 직선(회귀선) 형태의 모델, y = ax+b
회귀계수 : a, b는 최소 제곱법으로 추정, 회귀선과 각 관측치와의 거리의 제곱합이 가장 최소가 되는 회귀선 추정
회귀 모형의 유의성 검정 :
1) 각 독립 변수 x가 종속 변수 y를 설명하기에 유용한 변수인가는 회귀 계수 b에 대한 t검정을 통해 파악
귀무가설 : b는 0이다
대립가설 : b는 0이 아니다. (독립변수 x가 유용한 변수이다)
2) 모델의 전반적인 유의성 검정은 F검정
귀무가설 : b는 0이다
대립가설 : b는 0이 아니다
결정계수 coefficient of determination R제곱 : 0과 1사이의 값으로 추정된 회귀모형을 통해 설명되는 값
1에 가까울 수록 완벽하게 설명
잔차분석 residual analysis) : 회귀모형의 가정이 적절한 것인가 평가
1) 오차의 정규성 - 히스토그랩 또는 QQplot으로 확인 (라인에 붙어 있어야 정규)
2) 오차의 등분산성 - 잔차산점도로 확인 (일정한 패턴을 가지고 있어야 등분산)
3) 오차의 독립성 - 잔차산점도로 확인 (일정한 패턴을 가지고 있어야 등분산)
자동차 데이터
speed dist
4 2
4 10
7 4
7 22
R 코드 예제
> m<- lm(dist ~ speed, cars)
> m
(Intercept) speed
-17.579 3.932
이면 추정되는 회귀식은 y = -17.579 + 3.932x
>plot(cars$speed, cars$dist)
>abline(coef(m))
>lm(formula = dist ~ speed, data = cars)
Estimate t value p-value
(intercept) -17.5791 -2.601 0.0123 *
speed 3.9324 9.464 1.49e-12 ***
R-squared : 0.6511 Adjusted R-squared : 0.6438
F-statistic : 89.57, p-value : 1.49e-12 ***